How long is the coastline of New Zealand?

DOC says it is about 15,000 km https://www.doc.govt.nz/globalassets/documents/science-and-technical/docts10.pdf, Navigatus Consulting use 15,000km in the MOSRA15 model http://mosra15.navigatusconsulting.com/login, NZ post says between 15,000 and 18,000 km https://collectables.nzpost.co.nz/new-zealand-coastlines/, and NIWA says 18,000km https://environment.govt.nz/publications/a-classification-of-new-zealands-coastal-hydrosystems/. Which is it?
The answer is… both? …neither? It depends on how you measure it. It turns out that its often not whether you include estuaries or measure at high or low tide (which were my first thought). It’s how small a measuring stick you use.
Measurement
The way humans measure anything, not just length, is we have a unit of measurement. Examples of this are the second for time, the kilogram for mass, and the metre for length. However, in the real world these units are often too exact to be useful (second is defined as being equal to the time duration of 9,192,631,770 periods of the radiation corresponding to the transition between the two hyperfine levels of the fundamental unperturbed ground-state of the caesium-133 atom, see more at: https://www.measurement.govt.nz/metrology/si-units/second/). So, to get a ‘good enough’ estimate we allow for small discrepancies to happen as long as we are near enough. A ruler is not EXACTLY 30 cm, but it is near enough.
To measure coastline the most common approach is to use a fairly large unit of measurement (e.g., 20 kilometres) and enclose the coastline with units so that no land is outside of the ‘km box’ and the least amount of non-land is inside. This gives an approximation of the coastline. However, the smaller the unit used, the larger the result.
The Mathematics of Coastlines
This is a branch of mathematics called fractals, where a shape has infinitely complex patterns that are self-similar across different scales (this means when you zoom in on a section of the perimeter it looks the same as the zoomed-out version). 2D fractals have a finite area but an infinite perimeter. Whilst coastlines are not fractals, they almost are.
As shown is the figure below, the smaller the unit the larger the coastline. Which brings us back to our original question. Who is right? Probably neither, but that is fine. Both 15,000km and 18,000km are approximations of a value that is next to impossible to measure. Both of these numbers and useful as they are the best we can get and could be used in complex mathematical models that give nearly correct outputs.
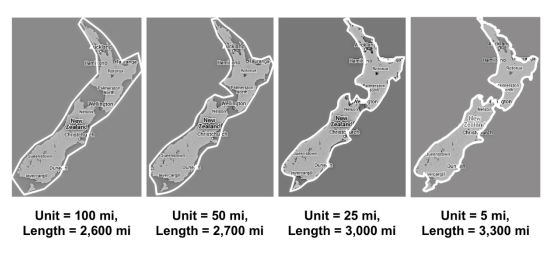
Here at Navigatus we understand the models are just that, models. They cannot and should not be exactly the same as the thing being modelled. The best outcome is often to get a close to correct approximation and use that as it is quicker to calculate, easy to work with, and nearly always is so close to the real answer that it doesn’t matter. The same principles apply with risk management. Often it is either impossible or infeasible to eliminate risk of all kinds. In these situations being conscious of the risks that are being allowed to remain and minimizing them as much as practicably possible is often a better solution than attempting and failing to eliminate that risk. To see more of the modelling Navigatus has done in the past go to: https://www.navigatusconsulting.com/list-example-projects/

Comments
No comments yet.